Twin Delayed Deep Deterministic Policy Gradient¶
Actions space: Continuous
References: Addressing Function Approximation Error in Actor-Critic Methods
Network Structure¶
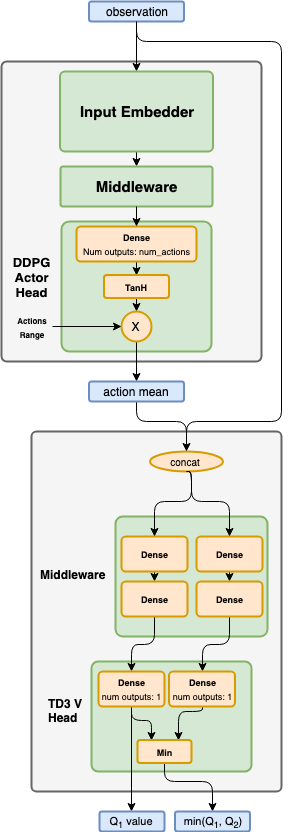
Algorithm Description¶
Choosing an action¶
Pass the current states through the actor network, and get an action mean vector \(\mu\). While in training phase, use a continuous exploration policy, such as a small zero-meaned gaussian noise, to add exploration noise to the action. When testing, use the mean vector \(\mu\) as-is.
Training the network¶
Start by sampling a batch of transitions from the experience replay.
To train the two critic networks, use the following targets:
\(y_t=r(s_t,a_t )+\gamma \cdot \min_{i=1,2} Q_{i}(s_{t+1},\mu(s_{t+1} )+[\mathcal{N}(0,\,\sigma^{2})]^{MAX\_NOISE}_{MIN\_NOISE})\)
First run the actor target network, using the next states as the inputs, and get \(\mu (s_{t+1} )\). Then, add a clipped gaussian noise to these actions, and clip the resulting actions to the actions space. Next, run the critic target networks using the next states and \(\mu (s_{t+1} )+[\mathcal{N}(0,\,\sigma^{2})]^{MAX\_NOISE}_{MIN\_NOISE}\), and use the minimum between the two critic networks predictions in order to calculate \(y_t\) according to the equation above. To train the networks, use the current states and actions as the inputs, and \(y_t\) as the targets.
To train the actor network, use the following equation:
\(\nabla_{\theta^\mu } J \approx E_{s_t \tilde{} \rho^\beta } [\nabla_a Q_{1}(s,a)|_{s=s_t,a=\mu (s_t ) } \cdot \nabla_{\theta^\mu} \mu(s)|_{s=s_t} ]\)
Use the actor’s online network to get the action mean values using the current states as the inputs. Then, use the first critic’s online network in order to get the gradients of the critic output with respect to the action mean values \(\nabla _a Q_{1}(s,a)|_{s=s_t,a=\mu(s_t ) }\). Using the chain rule, calculate the gradients of the actor’s output, with respect to the actor weights, given \(\nabla_a Q(s,a)\). Finally, apply those gradients to the actor network.
The actor’s training is done at a slower frequency than the critic’s training, in order to allow the critic to better fit the current policy, before exercising the critic in order to train the actor. Following the same, delayed, actor’s training cadence, do a soft update of the critic and actor target networks’ weights from the online networks.
-
class
rl_coach.agents.td3_agent.TD3AlgorithmParameters[source]¶ - Parameters
num_steps_between_copying_online_weights_to_target – (StepMethod) The number of steps between copying the online network weights to the target network weights.
rate_for_copying_weights_to_target – (float) When copying the online network weights to the target network weights, a soft update will be used, which weight the new online network weights by rate_for_copying_weights_to_target
num_consecutive_playing_steps – (StepMethod) The number of consecutive steps to act between every two training iterations
use_target_network_for_evaluation – (bool) If set to True, the target network will be used for predicting the actions when choosing actions to act. Since the target network weights change more slowly, the predicted actions will be more consistent.
action_penalty – (float) The amount by which to penalize the network on high action feature (pre-activation) values. This can prevent the actions features from saturating the TanH activation function, and therefore prevent the gradients from becoming very low.
clip_critic_targets – (Tuple[float, float] or None) The range to clip the critic target to in order to prevent overestimation of the action values.
use_non_zero_discount_for_terminal_states – (bool) If set to True, the discount factor will be used for terminal states to bootstrap the next predicted state values. If set to False, the terminal states reward will be taken as the target return for the network.