Rainbow¶
Actions space: Discrete
References: Rainbow: Combining Improvements in Deep Reinforcement Learning
Network Structure¶
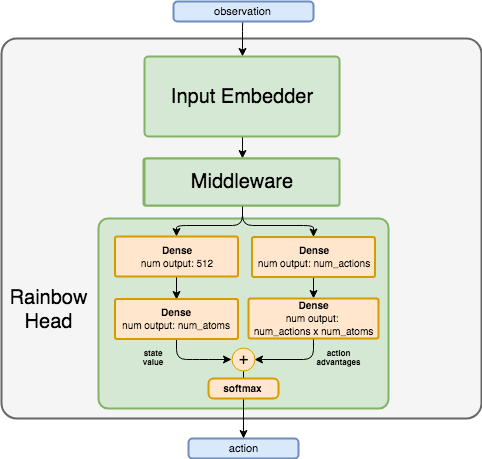
Algorithm Description¶
Rainbow combines 6 recent advancements in reinforcement learning:
N-step returns
Distributional state-action value learning
Dueling networks
Noisy Networks
Double DQN
Prioritized Experience Replay
Training the network¶
Sample a batch of transitions from the replay buffer.
The Bellman update is projected to the set of atoms representing the \(Q\) values distribution, such that the \(i-th\) component of the projected update is calculated as follows:
\((\Phi \hat{T} Z_{\theta}(s_t,a_t))_i=\sum_{j=0}^{N-1}\Big[1-\frac{\lvert[\hat{T}_{z_{j}}]^{V_{MAX}}_{V_{MIN}}-z_i\rvert}{\Delta z}\Big]^1_0 \ p_j(s_{t+1}, \pi(s_{t+1}))\)
where: * \([ \cdot ]\) bounds its argument in the range \([a, b]\) * \(\hat{T}_{z_{j}}\) is the Bellman update for atom \(z_j\): \(\hat{T}_{z_{j}} := r_t+\gamma r_{t+1} + ... + \gamma r_{t+n-1} + \gamma^{n-1} z_j\)
Network is trained with the cross entropy loss between the resulting probability distribution and the target probability distribution. Only the target of the actions that were actually taken is updated.
Once in every few thousand steps, weights are copied from the online network to the target network.
After every training step, the priorities of the batch transitions are updated in the prioritized replay buffer using the KL divergence loss that is returned from the network.
-
class
rl_coach.agents.rainbow_dqn_agent.RainbowDQNAlgorithmParameters[source]¶ - Parameters
n_step – (int) The number of steps to bootstrap the network over. The first N-1 steps actual rewards will be accumulated using an exponentially growing discount factor, and the Nth step will be bootstrapped from the network prediction.
store_transitions_only_when_episodes_are_terminated – (bool) If set to True, the transitions will be stored in an Episode object until the episode ends, and just then written to the memory. This is useful since we want to calculate the N-step discounted rewards before saving the transitions into the memory, and to do so we need the entire episode first.