Mixed Monte Carlo¶
Actions space: Discrete
References: Count-Based Exploration with Neural Density Models
Network Structure¶
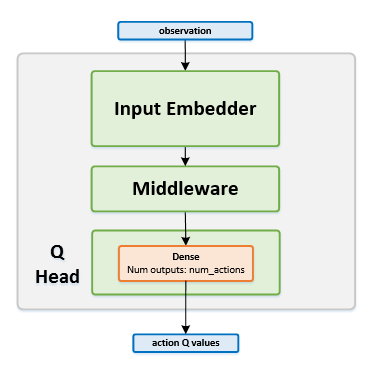
Algorithm Description¶
Training the network¶
In MMC, targets are calculated as a mixture between Double DQN targets and full Monte Carlo samples (total discounted returns).
The DDQN targets are calculated in the same manner as in the DDQN agent:
\(y_t^{DDQN}=r(s_t,a_t )+\gamma Q(s_{t+1},argmax_a Q(s_{t+1},a))\)
The Monte Carlo targets are calculated by summing up the discounted rewards across the entire episode:
\(y_t^{MC}=\sum_{j=0}^T\gamma^j r(s_{t+j},a_{t+j} )\)
A mixing ratio $alpha$ is then used to get the final targets:
\(y_t=(1-\alpha)\cdot y_t^{DDQN}+\alpha \cdot y_t^{MC}\)
Finally, the online network is trained using the current states as inputs, and the calculated targets. Once in every few thousand steps, copy the weights from the online network to the target network.